前言
外部排序用于待排序文件较大、内存无法一次性读取
外部排序原理
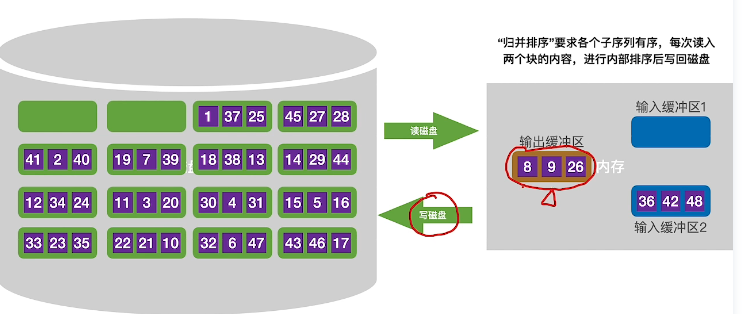
当数据元素较大时,通过在本地建立输入缓冲区和输出缓冲区,每次读取一小块数据进行排序后放回!
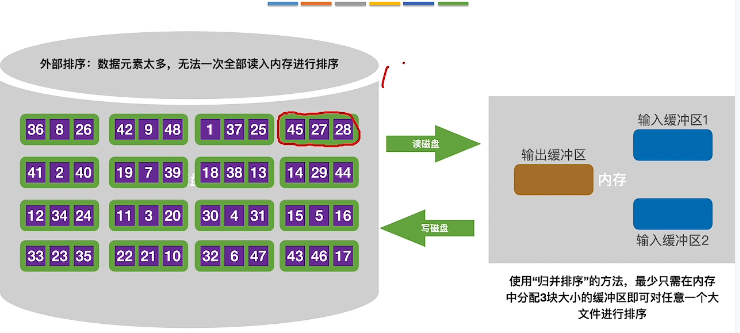
模拟
- 初始化数据分布如下
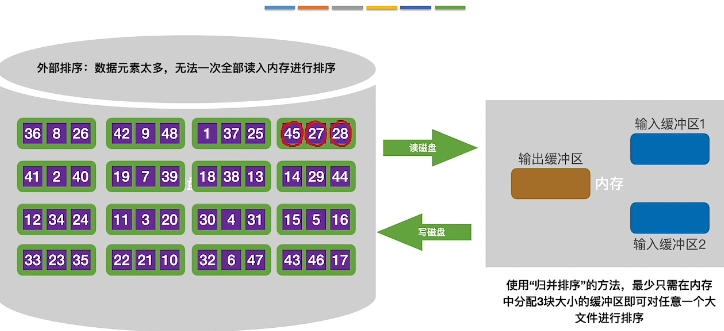
- 读入两块数据
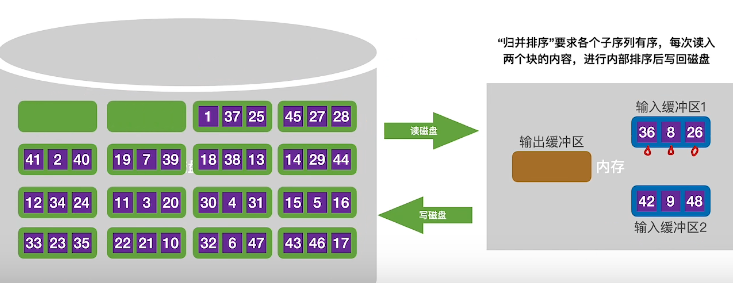
进行排序
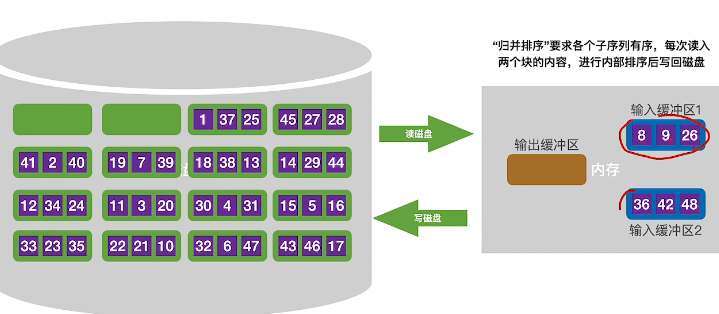
映射输出缓冲区,并写出两块数据
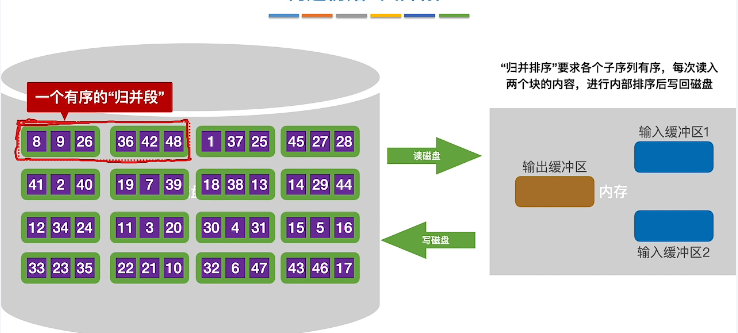
- 重复上述操作,构造归并段
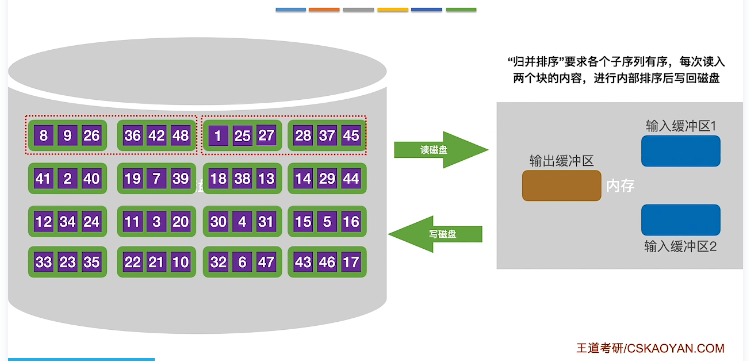
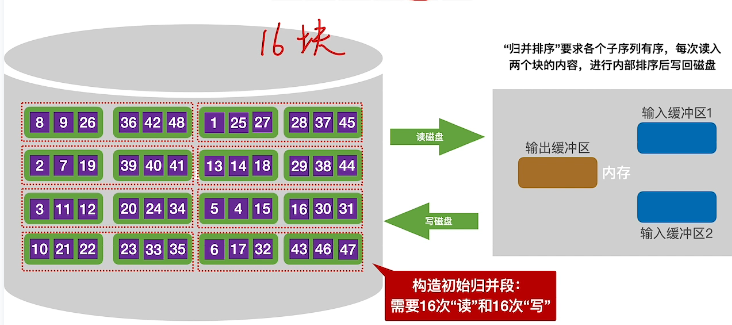
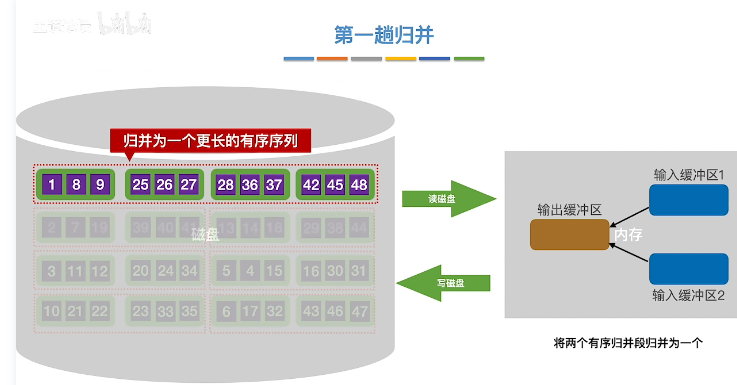
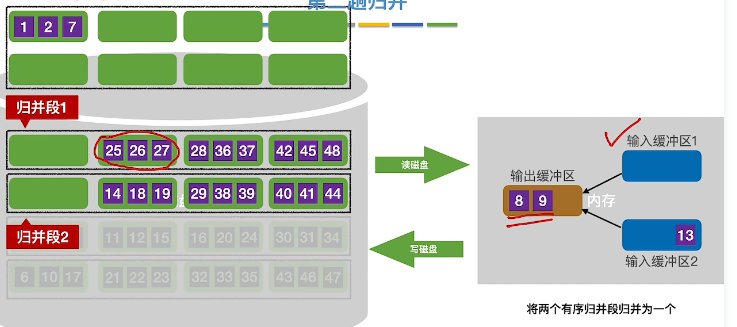
- 进行第一趟归并
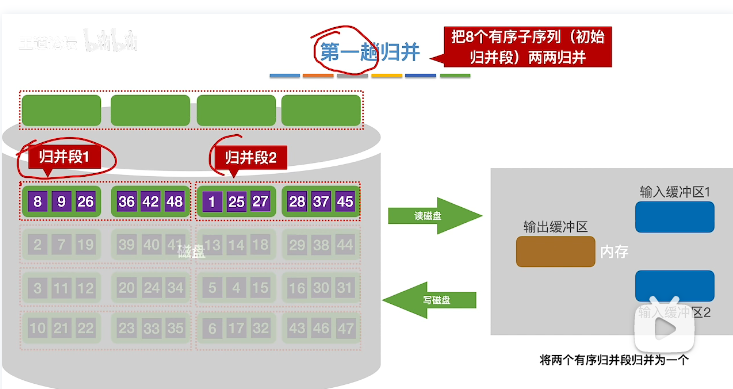
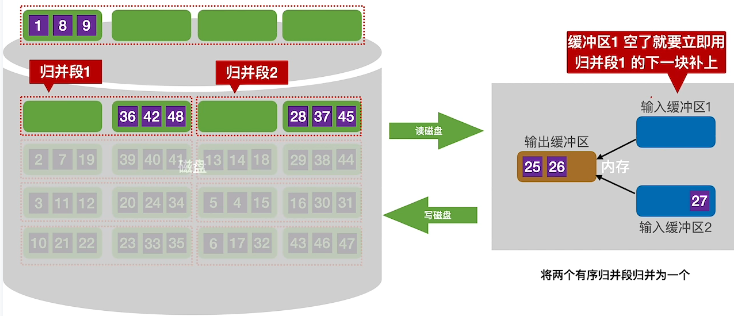
将两块归并段分别放入输入缓冲区
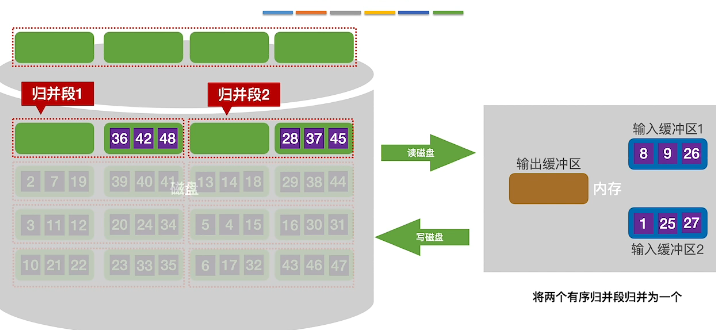
将输入缓冲区前三个放入到输出缓冲区中并输出
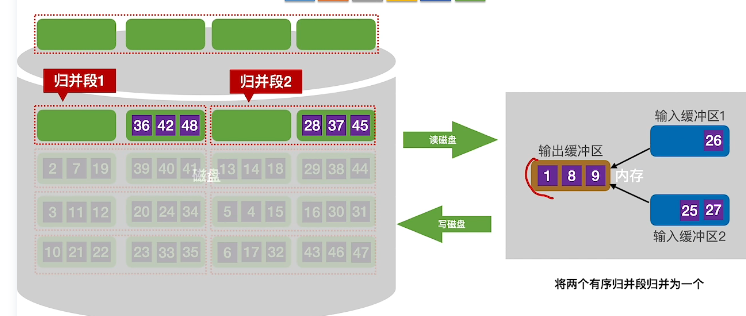
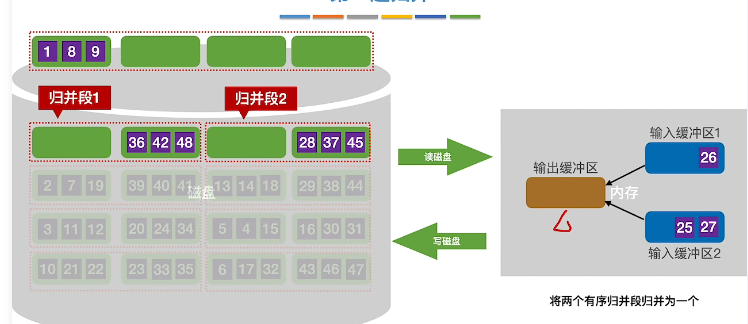
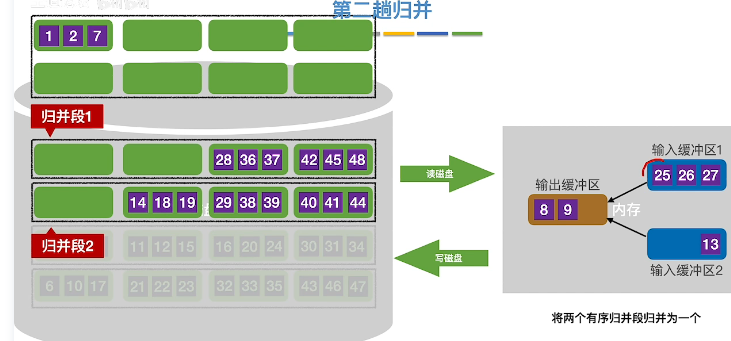
继续排序输入缓冲区,直到输入缓冲区无数据,此时读取一个新的磁盘块进入
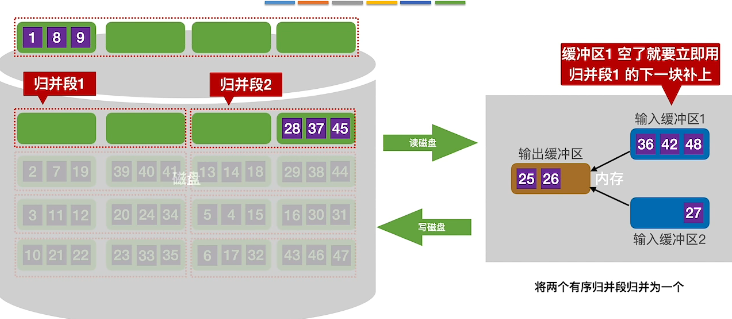
继续排序和输出,当输入缓冲区空了,继续读取下一个
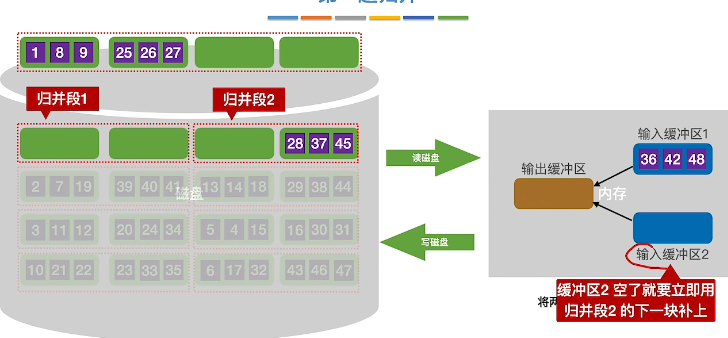
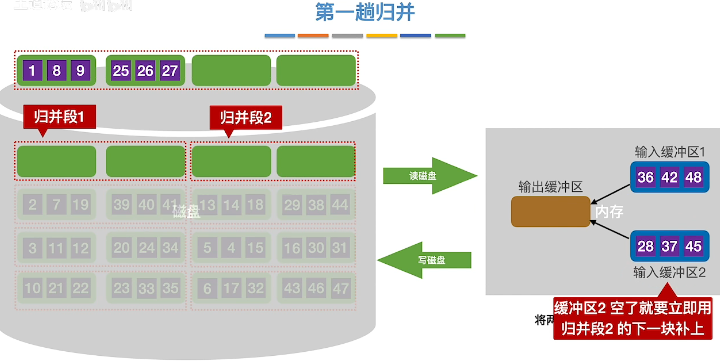
归并成新的归并段
重复上述操作,完成第二第三第四
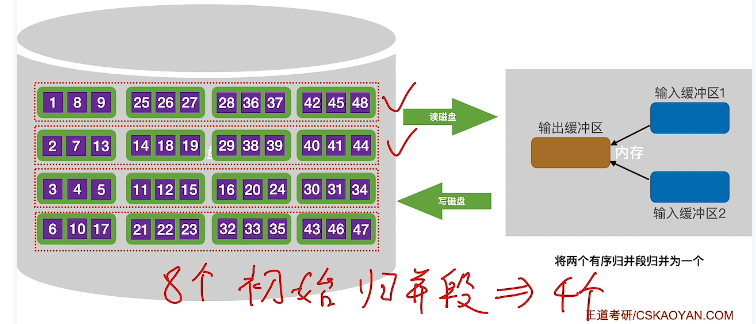
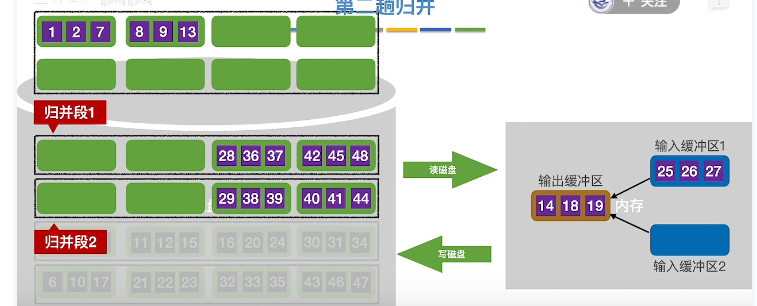
- 第二趟归并
初始值
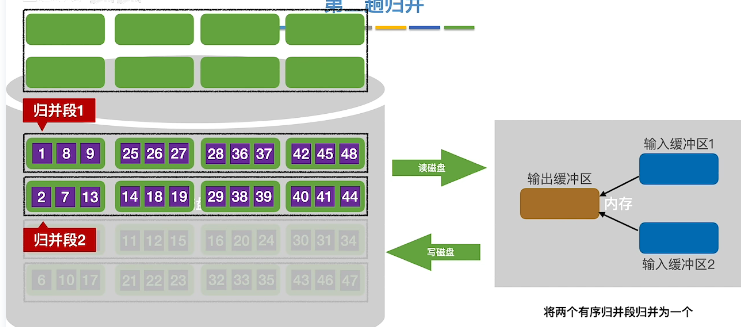
读入两个缓冲区
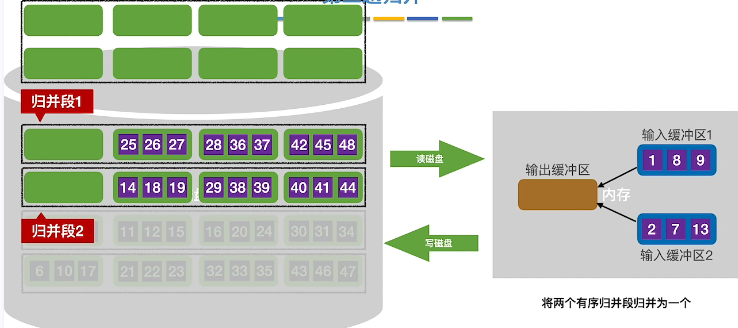
排序输出,空了补入新的缓冲区
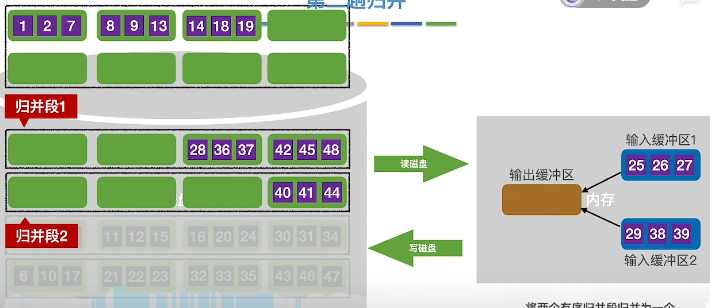
重复操作,完成后两个归并段归并
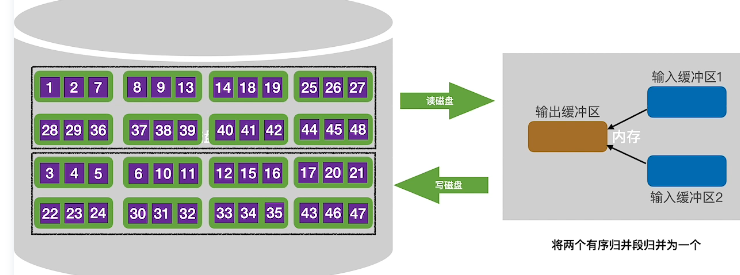
- 第三趟归并
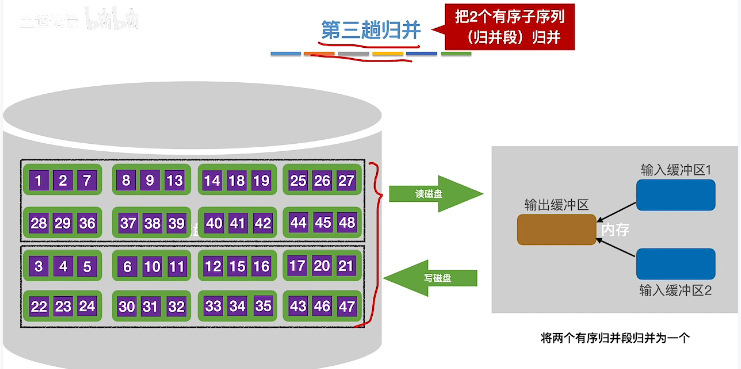
优化:多路归并
比如:2路变成4路
2路: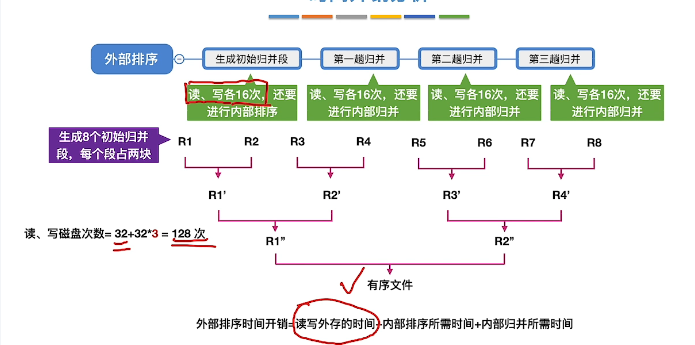
4路: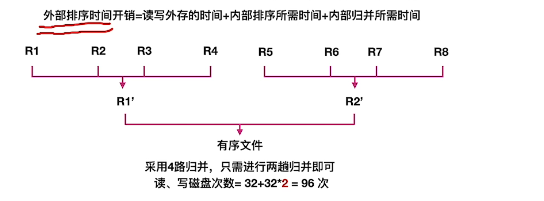
采用多路归并可以减少归并趟数,从而减少了磁盘I0读写次数
对于r个初始归并段,做k路归并
若树高h,则归并次数 = h - 1 = logkr
结论:
- 增加归并路数k
- 较少初始归并段数量r
败者树
使用k路平衡归并策略,选出一个最小元素需要对比关键字k-1次,导致内部归并所需时间增加
败者树:
比如100个人,选出一个最强者,如果比较99次,极其浪费。败者树采用篮球比赛的队伍决胜,比如:
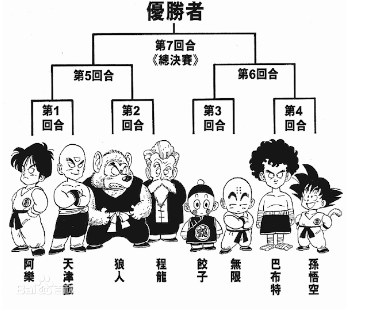
模拟
- 初始化,此时存在8个归并段
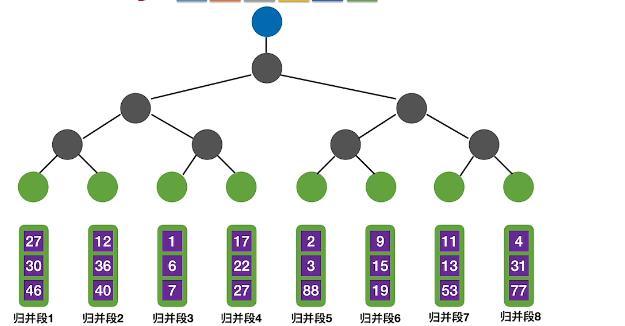
- 赋值
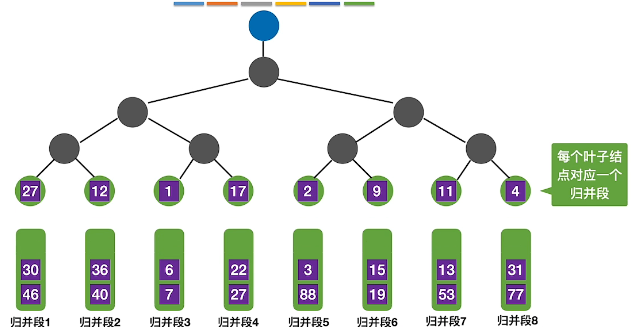
- 进行比较,胜利的进入,分支节点记录失败者来自哪个归并段,根节点记录冠军
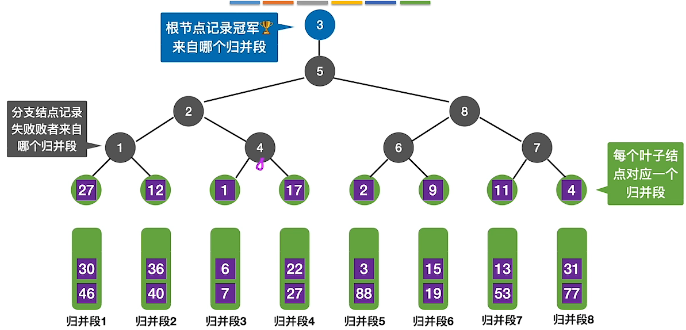
- 取出最小值,第5个归并段,即1
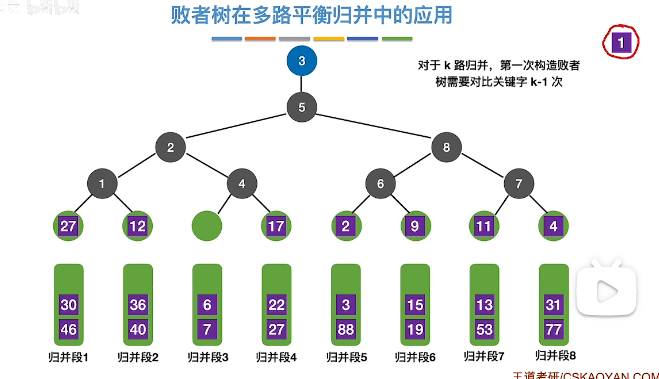
- 新值进入被取走的位置
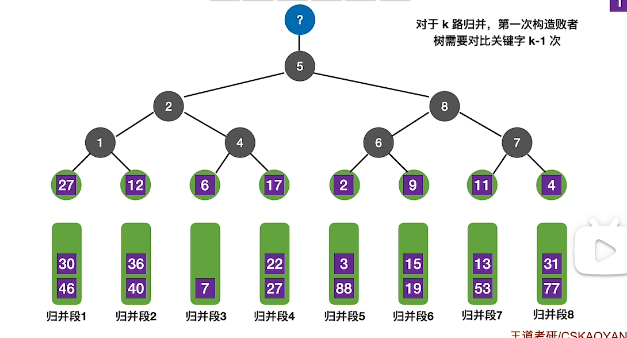
k路归并的败者树深度为log2k,最多需要log2k次比较
置换-选择排序
模拟
- 初始化
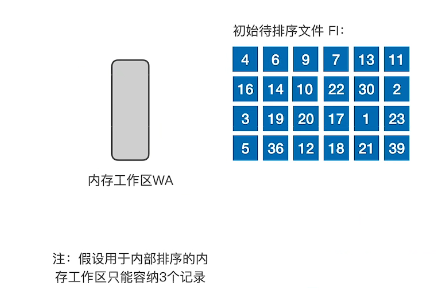
- 读入3个,填满
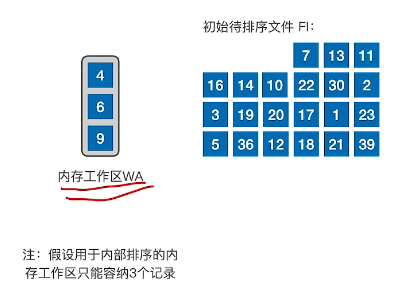
- 取出最小的数字到归并段,并记录值
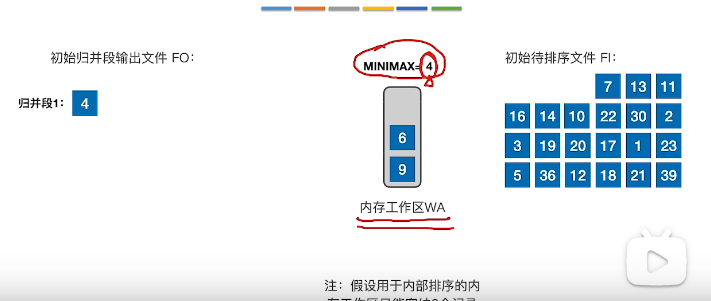
- 读入下一个,并将最接近4的数字取出到归并段,如6,然后记录minmax = 6
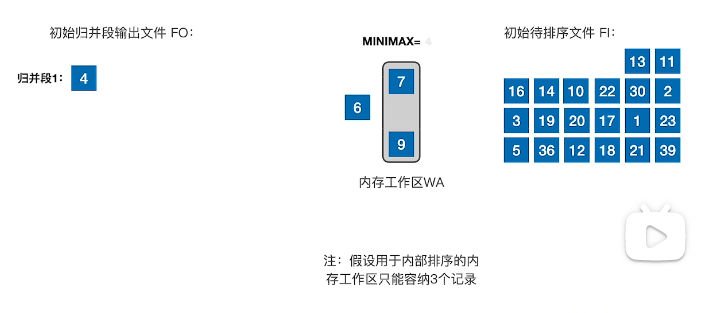
- 移7记录7
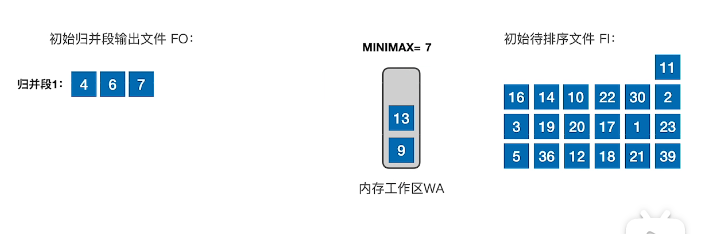
- 当移入10时,此时minmax是上一次的13,移入大的14,并且记录14
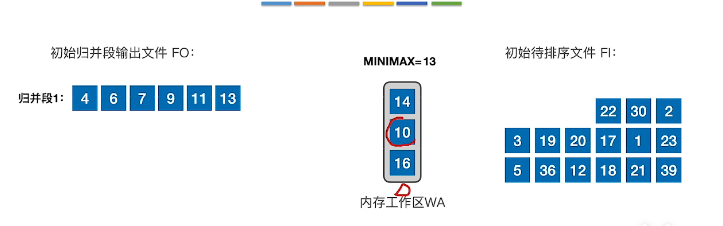
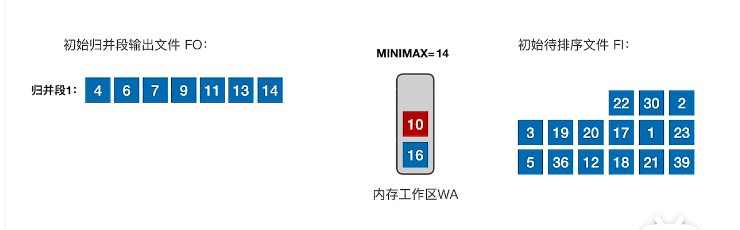
- 当minmax = 30,此时内存工作区没有大于30的数字时,第一个归并段到此为止,创建第二个归并段
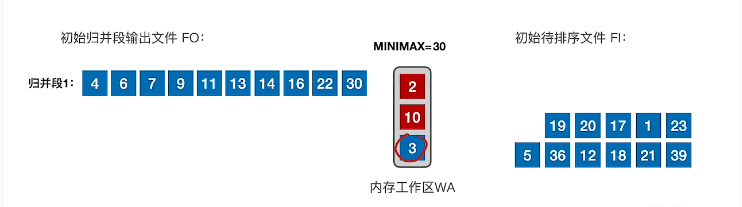
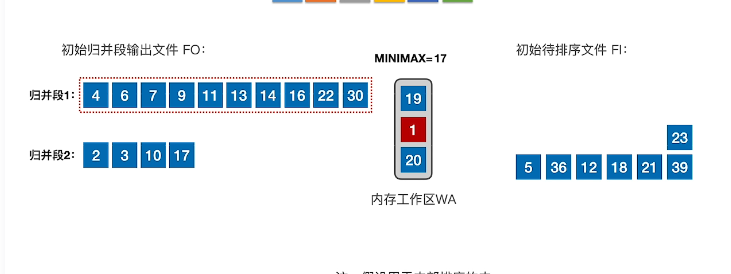
- 最终
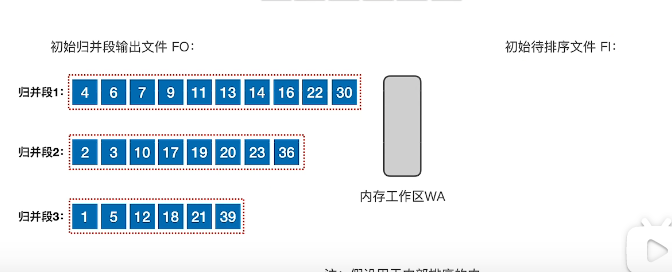
最佳归并数
引出:归并段长度可能不同

普通归并情况
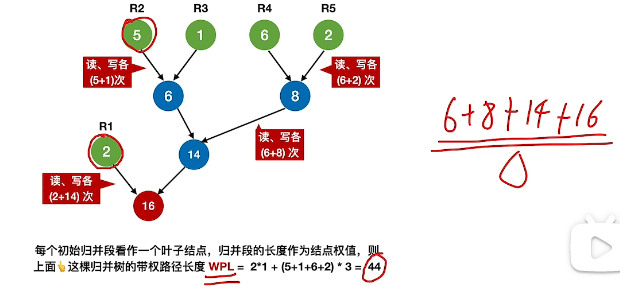
最佳归并数构建
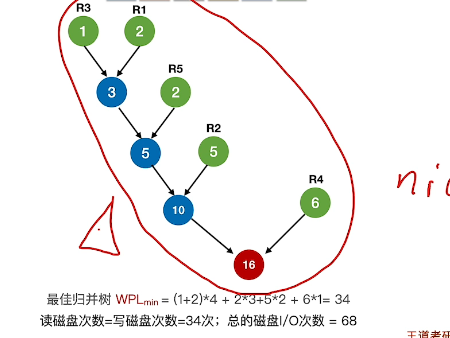
三路构建
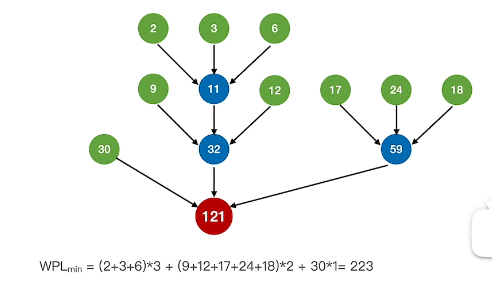
对于K叉归并,若初始归并段的数量无法构建成严格的k叉归并树,则需要补充几个长度为0的虚段
虚段添加










