题目
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
1
2
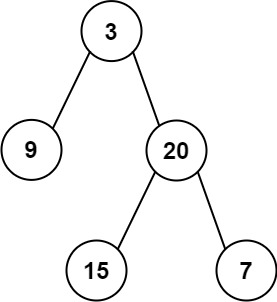
| Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
|
示例 2:
1
2
| Input: preorder = [-1], inorder = [-1]
Output: [-1]
|
限制:
解法一:分治
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.empty()){
return NULL;
}
// 对数组进行划分
int currentVal = preorder[0];
TreeNode* tree = new TreeNode(currentVal);
// 划分左右中序结果
int flag = 0;vector<int> leftInorder,rightInorder;
for(int v:inorder){
if(v==currentVal){
flag = 1;
continue;
}
if(flag == 0){
leftInorder.push_back(v);
}else{
rightInorder.push_back(v);
}
}
// 划分左右中序结果
vector<int> leftPreorder,rightPreorder;flag = 0;
for(int i=1;i<preorder.size();i++){
if(flag<leftInorder.size()){
flag++;
leftPreorder.push_back(preorder[i]);
}else{
rightPreorder.push_back(preorder[i]);
}
}
tree->left = buildTree(leftPreorder,leftInorder);
tree->right = buildTree(rightPreorder,rightInorder);
return tree;
}
};
|
结果:
1
2
3
4
5
6
7
8
9
10
| 执行用时:
116 ms
, 在所有 C++ 提交中击败了
5.19%
的用户
内存消耗:
157.4 MB
, 在所有 C++ 提交中击败了
5.04%
的用户
|
解法二:优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
private:
unordered_map<int, int> index;
public:
TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
};
|
结果
1
2
3
4
5
6
7
8
9
10
| 执行用时:
8 ms
, 在所有 C++ 提交中击败了
94.63%
的用户
内存消耗:
24.8 MB
, 在所有 C++ 提交中击败了
49.09%
的用户
|










