剑指 Offer 62. 圆圈中最后剩下的数字

题目内容

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

1 2	输入: n = 5, m = 3 输出: 3

示例 2：

1 2	输入: n = 10, m = 17 输出: 2

限制：

1 2	1 <= n <= 10^5 1 <= m <= 10^6

解法一:链表解决

思路:通过链表模拟


class Solution {

public:
    int lastRemaining(int n, int m) {
        if(m==1)return n-1;
        ListNode *l = new ListNode();
        ListNode *head = l;
        ListNode *lastHead;

        for(int i=0;i<n;i++){
            ListNode *temp = new ListNode();
            temp->val = i;
            l->next = temp;
            l = l->next;
        }
        l->next = head->next;
        head = head->next;
        int removeNumber = 0;
       while(1){
           if(head->val == head->next->val) break;
           if(removeNumber == m-1){
               lastHead->next = head->next;
               removeNumber=0;
           }else{
                removeNumber++;
           }
           lastHead = head;
           head = head->next;
       }
  
        return head->val;
    }
};

结果：超过时间限制。。。

分析：

如果单纯用链表模拟的话，时间复杂度是 O(nm)O(nm) 的，可以看下题目的数据范围，肯定是不能这么做的。关于运行时间的预估，经验是如果 n<10^5，那么 O(n^2)的解法耗时大概是几秒左右（当然时间复杂度会忽略常数，而且也有可能由于执行程序的机器性能的不同，O(n ^2)的实际耗时也有可能一秒多，也有可能十几秒）。本题由于 1 <= m <= 10^6，所以 O(nm)O(nm) 肯定是超时的。

解法二:动态规划

思路：

这个问题是以弗拉维奥·约瑟夫命名的，他是1世纪的一名犹太历史学家。他在自己的日记中写道，他和他的40个战友被罗马军队包围在洞中。他们讨论是自杀还是被俘，最终决定自杀，并以抽签的方式决定谁杀掉谁。约瑟夫斯和另外一个人是最后两个留下的人。约瑟夫斯说服了那个人，他们将向罗马军队投降，不再自杀。约瑟夫斯把他的存活归因于运气或天意，他不知道是哪一个。 —— 【约瑟夫问题】维基百科

利用数字表示11个人：

1、2、3、4、5、6、7、8、9、10、11

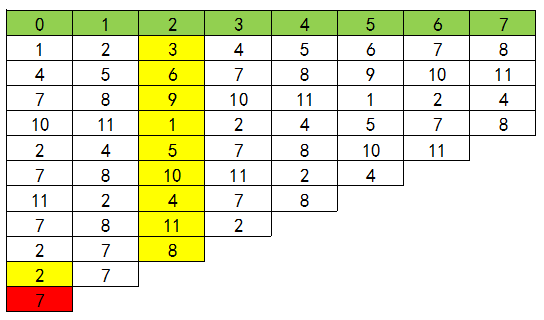
下图表示这一过程

class Solution {
public:
    int lastRemaining(int n, int m) {
        int res = 0;// 最后只剩下一位，坐标肯定是0
        for (int i = 2; i <= n; i++) {
            res = (res + m) % i;
        }
        return res;
    }
};

结果：

执行用时：
4 ms
, 在所有 C++ 提交中击败了
92.83%
的用户
内存消耗：
5.7 MB
, 在所有 C++ 提交中击败了
91.82%
的用户
通过测试用例：
36 / 36