前言
交换排序主要分为:简单选择排序和堆排序
思想:每一趟在待排序元素中选取关键字最小的元素。
应用:点名,哈希碰撞排序(统计词频)
一、简单选择排序
算法思想:
太简单了,还是看代码更快吧!
算法实现
1 | void sort(int A[],int n){ |
算法评估:
空间效率:$O(1)$
时间效率:
- $O(n^2)$
稳定性:是
二、堆排序
算法思想:
前缀知识:
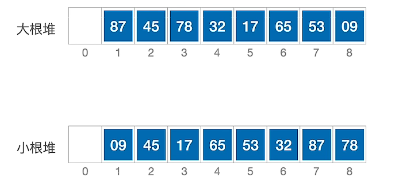
堆$L[1..n]$ 将其看作一课完全二叉树:
- 大根堆 $L[i] >= L[2i]$ 且 $L[i] >= L[2i+1]$ (最大元素在根节点)
- 小根堆 $L[i] <= L[2i]$ 且 $L[i] <= L[2i+1]$ (相反)
其中,对于 $i$
- $i$ 的左孩子 —— [2$i$]
- $i$ 的右孩子 —— [2$i$ +1]
- $i$ 的父节点 —— [$i$ /2]
- $i$ 所在的层次 —— $log_2(n+1) 或 log_2(n)+1$
存储视角:
逻辑视角: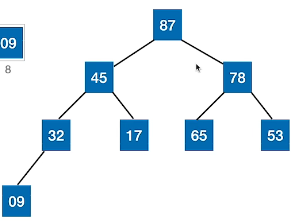
思路:
把所有非终端节点都检查一遍,是否满足大根堆的要求,如果不满足,则进行调整。
注:在顺序存储的完全二叉数中,非终端节点编号 $i<=[n/2]$
算法模拟:
1、建立大根堆方法
(1)、初始化序列如下,指针指向09
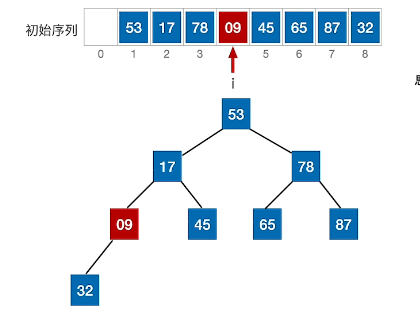
(2)、09与其左孩子比较,发现不满足根>=左、右,于是发生交换,同时指针往前移动
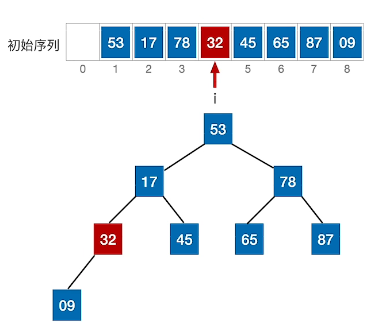
(3)、78与左右孩子进行比较,同理进行交换87
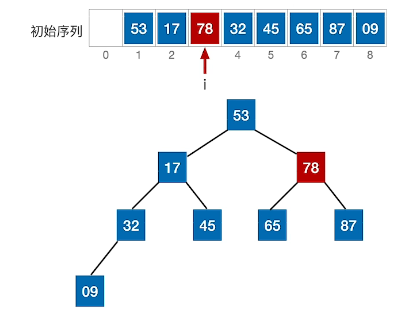
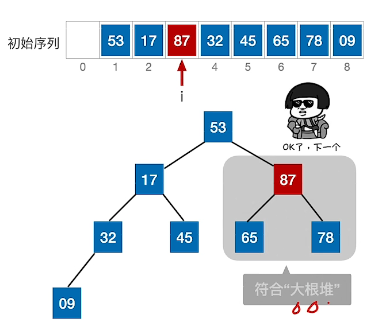
(4)、17与32和45比较,若皆小于,则交换较大的
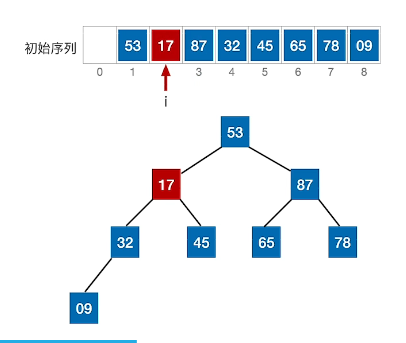
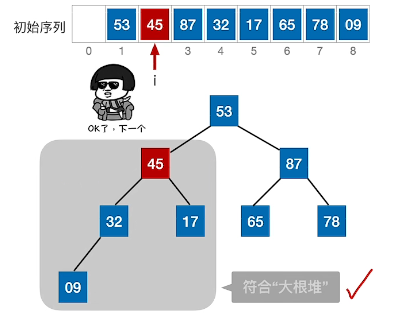
(5)、根节点53与左右孩子比较,交换87;交换后发现子树不符合要求,需要继续迭代交换直至符合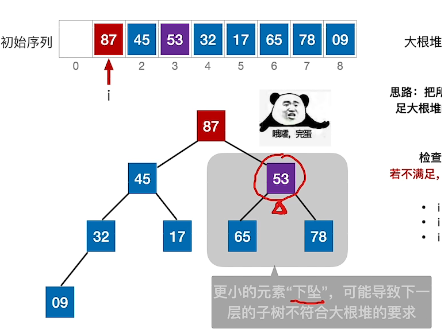
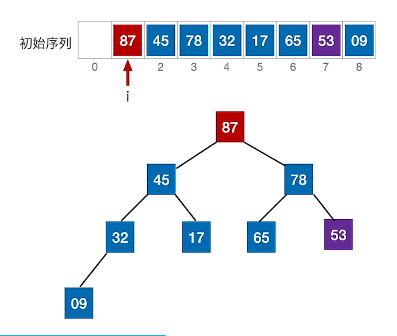
2、基于大根堆排序
1、每一趟将栈顶元素加入有序子序列(与最后一个元素交换)
建立大根堆后:
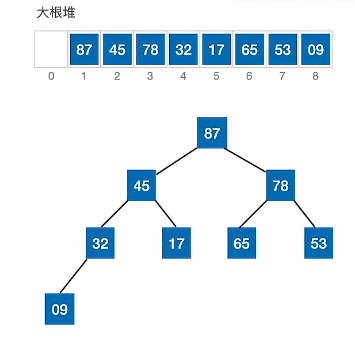
交换元素:
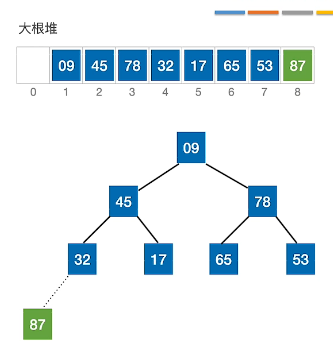
2、建立L[1…n-1]大根堆
初始状态:
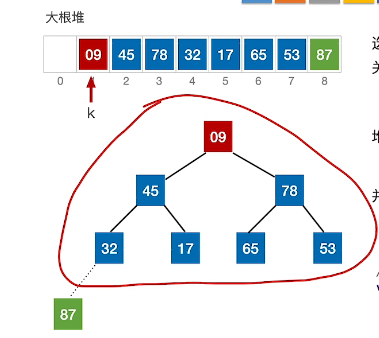
建立大根堆:
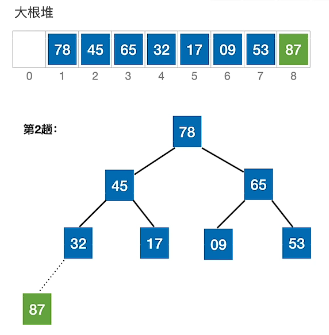
3、栈顶与倒数第二个元素交换
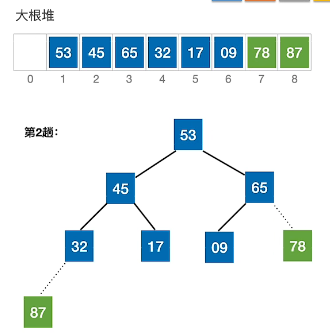
4、循环上面操作直至只剩下一个元素
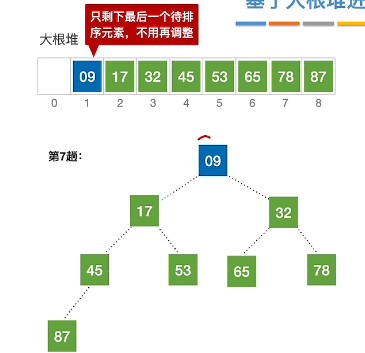
算法实现:
1 | // 建立大根堆 |
1 | // 堆排序的完整逻辑 |
算法评估:
空间效率:$O(1)$
时间效率:
- $O(n log_2n)$
稳定性:否









