交换排序(冒泡排序和快速排序)

前言

交换排序主要分为：冒泡排序和快速排序

思想：将序列中的两个元素关键字进行比较，后交换两个记录在序列中的位置

应用：队伍排队

一、冒泡排序

算法思想:

• 初始化下标为最后第一个，从后往前（或从前往后）两两比较相邻的元素，若（A[i-1]>A[i]）,则进行交换
• 下标往前移动

模拟实现：

算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

void sort(int A[],int n){
    int i,j;bool flag = flase;
    for(i = 0;i<n-1;i++){
        flag = false;
        for(j = n-1;j>i;j--){
            if(A[j-1] > A[j]){
                swap(A[j-1],A[j]);
                flag = true;
            }
        }

        if(! flag)return ;
    }
}

算法评估：

空间效率：$O(1)$
时间效率：

• $O(n^2)$

稳定性：是

二、快速排序

算法思想:

• 基于分治法
• 流程:
  • 在待排序表$L[1…n]$中任取一个元素pivot作为枢轴（通常选取首元素）
  • 通过一趟排序划分成独立的两部分（$L[1…K-1]$ 和 $L[k+1…n]$）,使得 $L[1…K-1]$ 都小于pivot,$L[k+1…n]$ 都大于pivot，则确定了pivot的位置
  • 接着对两部分分别进行递规上面的操作，使得每部分只有一个元素或为空

模拟实现：

第一轮

1、选择49（首部）作为枢轴，初始化指针low和hight为首尾部

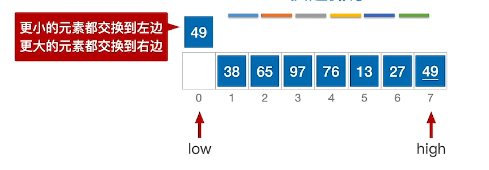
2、比较hight指针指向的值和枢轴，发现大于或等于49，则high指针向左移动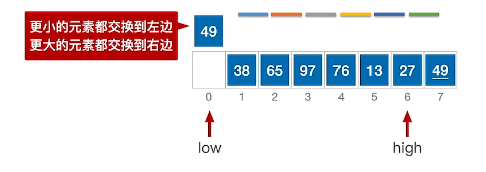

3、比较high指向的27对比枢轴49，发现小于，则将high指针指向的值赋值到low指针指向位置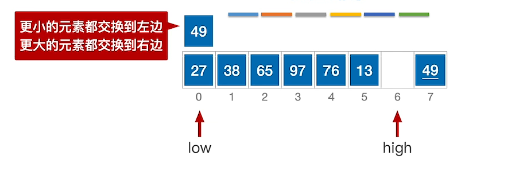

4、交替操作low指针，发现27小于49枢轴，继续向右移动low指针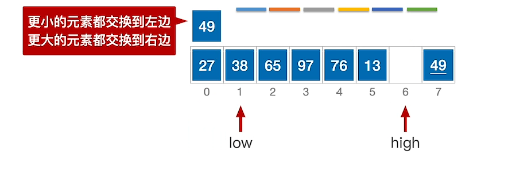

5、发现38还是小于49，继续移动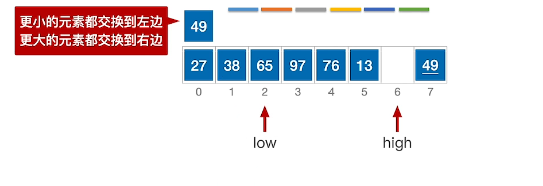

6、发现65大于49枢轴，于是将low指向的值赋值到high指针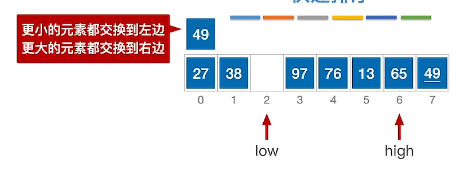

7、继续交替high和low指针保持上面的操作，直至两者相等

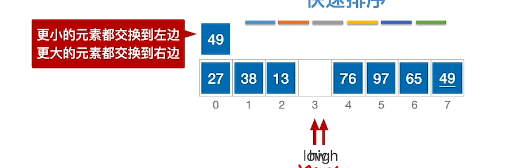
8、此时即可确定low指针位置为枢轴的最终位置

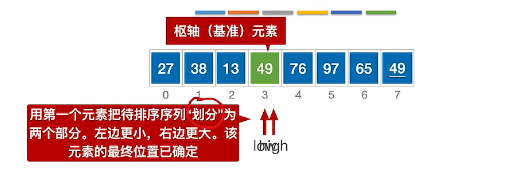
9、递规枢轴两边部分，使得每个枢轴都在最终位置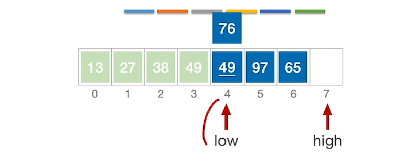

算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

void sort(int A[],int low,int high){
  if(low<high){
    int pivotpos = partition(A,low,high);
    sort(A,low,pivotpos-1);
    sort(A,prvotpos+1,high);
  }
}

int partition(int A[],int low,int high){
  int pivot = A[low]; // 选取一个元素作为枢轴
  while(low<high){
    while(low < high && A[high] >= pivot) --high;
    A[low] = A[high];
    while(low < high && A[low] <= pivot) ++low;
    A[high] = A[low];
  }
  A[low] = pivot;
  return low;
}

算法评估：

空间效率：

• 最坏 $O(n)$
• 平均 $O(log_2n)$

时间效率：

• 最坏 $O(n^2)$ =>两个区域包含n-1和0个元素，不对称情况下；或有序情况
• 平均 $O(n*log_2n)$

稳定性：否

快速排序是所有内部排序算法中平均性能最优的排序算法！