原理
摩尔投票法的基本思想很简单,在每一轮投票过程中,从数组中找出一对不同的元素,将其从数组中删除。
这样不断的删除直到无法再进行投票,如果数组为空,则没有任何元素出现的次数超过该数组长度的一半。
如果只存在一种元素,那么这个元素则可能为目标元素。
理解
用一个很好的例子可以介绍一下!
假设有一个擂台,有一组人,每个人有编号,相同编号为一组,依次上场,没人时上去的便是擂主(x),若有人,编号相同则继续站着(台上总人数+1),若不同,假设每个人战斗力相同,都同归于尽,则台上总人数-1;那么到最后站着的肯定是人数占绝对优势的那一组啦~对应的编号就是答案
1 | class Solution: |
例子
设输入数组 nums 的众数为 x ,数组长度为 n 。
推论一: 若记 众数 的票数为 +1 ,非众数 的票数为 -1 ,则一定有所有数字的 票数和 > 0 。
推论二: 若数组的前 a 个数字的 票数和 =0 ,则 数组剩余 (n-a) 个数字的 票数和一定仍 >0 ,即后 (n−a) 个数字的 众数仍为 xx 。
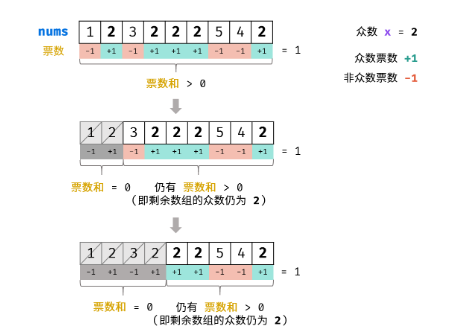
算法流程:
- 1.初始化: 票数统计 votes = 0 , 众数 x;
- 2.循环: 遍历数组 nums 中的每个数字 num ;
- 当 票数 votes 等于 0 ,则假设当前数字 num 是众数;
- 当 num = x 时,票数 votes 自增 1 ;当 num != x 时,票数 votes 自减 1 ;
- 3.返回值: 返回 x 即可;
1 | class Solution { |
相关题目
| 序号 | 题目内容 |
|---|---|
| 1 | 招式_剑指Offer 39. 数组中出现次数超过一半的数字 |









